
Just as understanding binary numbers is important, so is understanding hexadecimal or hex numbers. Before we go into any detail about hexadecimal numbers, I strongly suggest you read the post on binary numbers.
In it, you’ll learn why binary numbers are used in digital systems. This will help you understand why hex numbers also often appear in digital systems. You’ll also get a quick review of the decimal system (and number systems in general). Finally, you’ll learn how to read binary, which will help you understand how to translate from binary to hex.
As I said before, if you’re new to digital electronics, it’s a must read.
And if you’re not so new it’s a good review.
Let’s break the hex and learn about hexadecimal numbers!
Hexadecimal Number Basics
After binary numbers, hex numbers or base 16 numbers are the most important in digital applications.
The word hexadecimal comes from the Greek root hex – which means six, and the Latin root deci – meaning ten. Hence, the word hexadecimal refers to sixteen.
Hexadecimal numbers use a base 16 system which means that the positional multipliers in the hex system are powers of 16: 160 = 1, 161 = 16, 162 = 256 and so on. This is just like the decimal system were all familiar with, only instead of powers of 10 we’re dealing with powers of 16.
The chart below will come in handy for figuring out various powers of 16. My, how quickly they grow!
Note that MSD stands for most significant digit and LSD stands for least significant digit. Sorry for the disappointment, LSD is not a drug — at least not in this post.

Figure 1: various powers of 16.
The first 9 digits in the hexadecimal system are the same digits 0-9 that you’re familiar with. However, the next 6 are represent by the first few letters of the alphabet: A, B, C, D, E, and F.
The first 16 digits on the hex system are given in the chart below along with their decimal and binary equivalents.
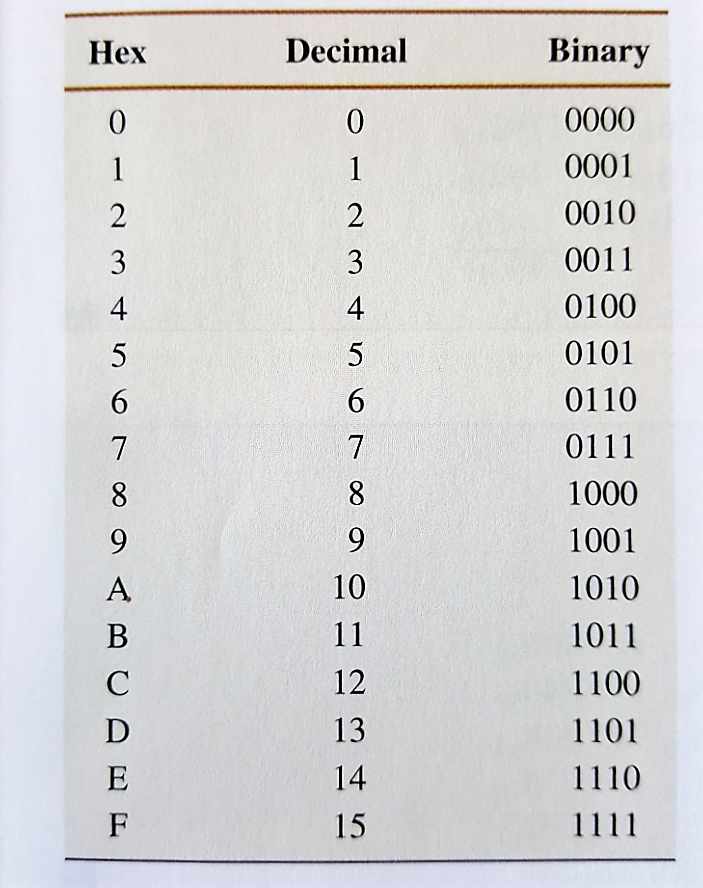
Figure 2: hex numbers and their decimal and binary equivalents.
If you’re not too familiar with the hexadecimal system, the use of letters to represent numbers may seem odd at first. Keep in mind though that any number system is only a set of sequential symbols. The form of the symbols is unimportant if you understand what they mean.
Remember also, that regardless of the number system, each digit must be represented by a single symbol.
Ever dreamed of being Iron Man, having the ability to build anything, anytime? Try Academy for Arduino!

If we were to use the symbols that make the number ten in decimal (rather than A) when writing numbers in hex, it would be hard to tell whether we were referring to 10 in decimal, or 10 in hex which equals 16 in decimal.
There is also perhaps an even more important reason for this, which we’ll disclose in the next section.
Why Use Hexadecimal Numbers?
Right now, it may be easy to think something like why bother with hex numbers? Base 16 is weird and seems complicated…
Or maybe you’ve already figured out the virtues of using hexadecimal numbers. If not, you will in a minute.
The translation from hex to binary in figure 2 suggest a very important reason hex numbers are popular.
Hexadecimal numbers are way more compact than binary and more compact than decimal numbers. Hex numbers pack more information into fewer digits.
Also, binary numbers are difficult to read and write because it is easy to drop or transpose a bit.
Because of this, hexadecimal is widely used in computer and microprocessor applications.
You’ve undoubtedly been faced with a blue screen on your computer after a crash. In addition, you’ll often see a cryptic message along with some hex numbers like 0xa56b170f.
The hex numbers refer to memory locations and data. If the PC was to spit it out in binary, the whole screen would be filled with 1’s and 0’s.
The prefix 0x tells us that the number is a hex number. The programming languages C and Java use this notation, but you may also see a hex number with the prefix 0h.
Almost all computer data sizes are multiples of 4. Since base 16 is a power of 2 (like 4), converting from binary to hex and vice versa is trivial, as we’ll see in a minute.
Converting Binary Numbers to Hexadecimal Numbers
As usual, the easiest way to convert a binary number to a hex number or vice versa is to use a calculator. However, you should be able to do it almost as fast after reading this section.
You should know all the hexadecimal numbers from 0 to F (0 to 15).
Figure 2 shows us that for every possible 4-bit binary number, there is a hex equivalent.
To convert a binary number to a hex number, simply break the binary number into 4-bit groups, starting with the LSB (right-most bit). Then replace each 4-bit group with its hexadecimal equivalent.
As you move to the left, you may notice that you have less than 4 binary digits left in the last group.
No sweat. Just pad the last group with enough leading zeros to reach 4 bits, then convert to hex.
Let’s do a couple examples to illustrate this.
Ex.1
Convert 1100101001010111 to hexadecimal.
Solution:
First, we break the binary number into groups of 4 bits:
1100 1010 0101 0111
Next, we simply find the hex equivalents of each of the groups of 4 binary digits, starting at the left:
1100 1010 0101 0111
| | | |
C A 5 7
1100 = 12 in decimal which is C in hex. Following a similar approach, we get A for the next group, 5 for the next and finally 7 for the last group.
Now we write CA57 or 0xCA57 so we know it’s a hex number. Wham, bam, thank you ma’am.
Ex. 2
Convert 11100010100110 to hex.
Solution:
Starting from the right (LSB), we break the binary number into groups of 4 bits:
11 1000 1010 0110
Since the group on the far left only has 2 digits, we pad it with 2 zeros:
0011 1000 1010 0110
Now, we take the hex equivalent of each of the 4 groups:
0011 1000 1010 0110
| | | |
3 8 A 6
Now, we write 0x38A6.
Note that while it’s obvious that if a string of digits contains any of the letters A through F the string is a hex number, not all hex numbers will contain letters. Therefore, to avoid confusion, especially in this case, it’s a good idea to use the 0x prefix when writing or typing hex numbers.
The general algorithm for converting a binary number to a hexadecimal number is as follows:
- Group the digits of the binary number into sets of 4 digits (or bits). Add leading zeros to last group of 4 on left if necessary.
- Convert the binary numbers in each set of 4 into the equivalent hex digits.
Converting Hexadecimal Numbers to Binary Numbers
The examples above suggest that this is also easy and trivial.
By simply doing the algorithm in reverse, we can convert a hexadecimal number to a binary number.
Let’s do a quick example.
Ex. 3
Convert 0xFF09 to binary.
Solution:
Starting at the far left, we write each hex digit in its equivalent binary format:
F = 1111, F = 1111, 0 = 0000, 9 = 1001
Stringing it all together, we get: 1111111100001001 or 1111 1111 0000 1001 if we break in up for easier reading.
The general algorithm for converting a binary number to a hexadecimal number is as follows:
- Write each hex digit as a 4-bit binary number
- Remember that 0 in hex is 0000 in binary!
Converting Decimal Numbers to Hex Numbers
Going from decimal to hex is a bit more complicated than going from binary to hex, but as we’ll see it’s similar to converting decimal to binary and not that hard to do.
There are two ways to convert decimal numbers to hexadecimal: sum of powers of 16 and repeated division by 16. Let’s talk about both.
Sum of Powers of 16
Also called sum of weighted hex digits method, this method is good for simpler conversions (up to about 3 hex digits).
For example, let’s convert 35 to hexadecimal using this method.
Upon inspection, we note that 35 = 32 + 3
We also note that (2 x 16) = 32 and that (3 x 1) = 3.
So, we have 2 sixteens (or 2 sixteens raised to the first power) and 3 ones (or 3 sixteens raised to the zeroth power).
Therefore 32 in decimal = 0x23.
Remember that any number raised to the zeroth power is one.
Repeated division by 16
The method above can become unwieldy for larger numbers.
Divide the decimal number by 16 and note the remainder. Be sure to write the remainder as a hexadecimal digit.
Repeat this process until the quotient is 0. The last remainder is the most significant digit of the hex number.
Ex. 4
Suppose we want to convert 31,581 to hexadecimal.
31,581 / 16 = 1973, remainder 13 (least significant digit, or LSD).
1,973 / 16 = 123, remainder 5
123 / 16 = 7, remainder 11
7 / 16 = 0, remainder 7 (most significant digit, or MSD)
Now we write all the remainders as hex digits: 13 = 0xD, 5 = 0x5, 11 = 0xB, 7 = 0x7
Listing them in proper order (MSD on far left; LSD on far right) gives us:
31,581 = 0x7B5D
Converting Hex Numbers to Decimal Numbers
One way to do this is to first convert the hex number into binary, then convert into decimal.
Another way to do this conversion is to multiply each digit by its power of 16 positional multiplier and add the products together.
The example below helps illustrate this.
Ex. 5
Convert 0x7C6 to decimal.
Solution:
First, we note each hex digit’s positional weight starting with the LSD: 6 has a weight of 160, C has a weight of 161, and 7 has a weight of 162.
Now we multiply each digit by its positional weight. We’ll start with the MSD:
7 x 162 = 7 x 256 = 1792
C x 161 = 12 x 16 = 192
6 x 160 = 6 x 1 = 6
Next, we’ll add up our results: 1792 + 192+ 6 = 1990
Taking the “Hex” Out of Hexadecimal Numbers
So now we know how hexadecimal numbers relate to digital circuits and how to convert hex to binary and vice versa. We also know how to convert hexadecimal numbers to decimal numbers and the reverse.
Since hex numbers are quite common in the world of computers and electronics, I’m sure they’ll come up again.
Only now you’ll know how to deal with them. And as a bonus, next time you experience the blue screen of death, you’ll be able to translate those hex digits into the memory address(es) where the error(s) occurred.
Comment and tell us what you prefer working with: hex or binary?
Or you can comment and let me know what other topics you’d like to hear about.
Until next time,
Keep geekin’
Ever dreamed of being Iron Man, having the ability to build anything, anytime? Try Academy for Arduino!

Electronics Tips & Tutorials Sent Directly to Your Inbox

Submit your email & you'll get:
- Exclusive content that I don't put on the blog
- The checklist 10 mistakes all electronics enthusiasts make (& how to avoid them)
- And more!
Leave a Reply